Models

This module contains recommender system algorithms including:

distributed models built in PySpark
neural networks build in PyTorch with distributed inference in PySpark
wrappers for commonly used recommender systems libraries and
models with non-distributed training and distributed inference in PySpark.

RePlay Recommenders

Algorithm	Implementation
Popular Recommender	PySpark
Popular By Users	PySpark
Wilson Recommender	PySpark
Random Recommender	PySpark
K-Nearest Neighbours	PySpark
Alternating Least Squares	PySpark
SLIM	PySpark
Word2Vec Recommender	PySpark
Association Rules Item-to-Item Recommender	PySpark
Cluster Recommender	PySpark
Neural Matrix Factorization	Python CPU/GPU
MultVAE	Python CPU/GPU
ADMM SLIM	Python CPU
Обертка Implicit	Python CPU
Обертка LightFM	Python CPU

To get more info on how to choose base model, please see this page.

Recommender interface

class replay.models.Recommender

Usual recommender class for models without features.

fit(log)

Fit a recommendation model

Parameters: log (DataFrame) – historical log of interactions [user_idx, item_idx, timestamp, relevance]
Return type: None
Returns

fit_predict(log, k, users=None, items=None, filter_seen_items=True)

Fit model and get recommendations

Parameters

log (DataFrame) – historical log of interactions [user_idx, item_idx, timestamp, relevance]
k (int) – number of recommendations for each user
users (Union[DataFrame, Iterable, None]) – users to create recommendations for dataframe containing [user_idx] or array-like; if None, recommend to all users from log
items (Union[DataFrame, Iterable, None]) – candidate items for recommendations dataframe containing [item_idx] or array-like; if None, take all items from log. If it contains new items, relevance for them will be 0.
filter_seen_items (bool) – flag to remove seen items from recommendations based on log.

Return type

DataFrame

Returns

recommendation dataframe [user_idx, item_idx, relevance]

get_features(ids)

Returns user or item feature vectors as a Column with type ArrayType

Parameters: ids (DataFrame) – Spark DataFrame with unique ids
Return type: Optional[Tuple[DataFrame, int]]
Returns: feature vectors. If a model does not have a vector for some ids they are not present in the final result.

predict(log, k, users=None, items=None, filter_seen_items=True)

Get recommendations

Parameters

log (DataFrame) – historical log of interactions [user_idx, item_idx, timestamp, relevance]
k (int) – number of recommendations for each user
users (Union[DataFrame, Iterable, None]) – users to create recommendations for dataframe containing [user_idx] or array-like; if None, recommend to all users from log
items (Union[DataFrame, Iterable, None]) – candidate items for recommendations dataframe containing [item_idx] or array-like; if None, take all items from log. If it contains new items, relevance for them will be 0.
filter_seen_items (bool) – flag to remove seen items from recommendations based on log.

Return type

DataFrame

Returns

recommendation dataframe [user_idx, item_idx, relevance]

predict_pairs(pairs, log=None)

Get recommendations for specific user-item pairs. If a model can’t produce recommendation for specific pair it is removed from the resulting dataframe.

Parameters

pairs (DataFrame) – dataframe with pairs to calculate relevance for, [user_idx, item_idx].
log (Optional[DataFrame]) – historical log of interactions [user_idx, item_idx, timestamp, relevance]

Return type

DataFrame

Returns

recommendation dataframe [user_idx, item_idx, relevance]

class replay.models.base_rec.BaseRecommender

Base recommender

optimize(train, test, user_features=None, item_features=None, param_borders=None, criterion=<replay.metrics.ndcg.NDCG object>, k=10, budget=10, new_study=True)

Searches best parameters with optuna.

Parameters

train (DataFrame) – train data
test (DataFrame) – test data
user_features (Optional[DataFrame]) – user features
item_features (Optional[DataFrame]) – item features
param_borders (Optional[Dict[str, List[Any]]]) – a dictionary with search borders, where key is the parameter name and value is the range of possible values {param: [low, high]}. In case of categorical parameters it is all possible values: {cat_param: [cat_1, cat_2, cat_3]}.
criterion (Metric) – metric to use for optimization
k (int) – recommendation list length
budget (int) – number of points to try
new_study (bool) – keep searching with previous study or start a new study

Return type

Optional[Dict[str, Any]]

Returns

dictionary with best parameters

Distributed models

Models with both training and inference implemented in pyspark.

Popular Recommender

class replay.models.PopRec(use_relevance=False)

Recommend objects using their popularity.

Popularity of an item is a probability that random user rated this item.

\[Popularity(i) = \dfrac{N_i}{N}\]

\(N_i\) - number of users who rated item \(i\)

\(N\) - total number of users

>>> import pandas as pd
>>> data_frame = pd.DataFrame({"user_idx": [1, 1, 2, 2, 3, 4], "item_idx": [1, 2, 2, 3, 3, 3], "relevance": [0.5, 1, 0.1, 0.8, 0.7, 1]})
>>> data_frame
   user_idx  item_idx  relevance
0         1         1        0.5
1         1         2        1.0
2         2         2        0.1
3         2         3        0.8
4         3         3        0.7
5         4         3        1.0

>>> from replay.utils import convert2spark
>>> data_frame = convert2spark(data_frame)

>>> res = PopRec().fit_predict(data_frame, 1)
>>> res.toPandas().sort_values("user_idx", ignore_index=True)
   user_idx  item_idx  relevance
0         1         3       0.75
1         2         1       0.25
2         3         2       0.50
3         4         2       0.50

>>> res = PopRec().fit_predict(data_frame, 1, filter_seen_items=False)
>>> res.toPandas().sort_values("user_idx", ignore_index=True)
   user_idx  item_idx  relevance
0         1         3       0.75
1         2         3       0.75
2         3         3       0.75
3         4         3       0.75

>>> res = PopRec(use_relevance=True).fit_predict(data_frame, 1)
>>> res.toPandas().sort_values("user_idx", ignore_index=True)
   user_idx  item_idx  relevance
0         1         3      0.625
1         2         1      0.125
2         3         2      0.275
3         4         2      0.275

User Popular Recommender

class replay.models.UserPopRec

Recommends old objects from each user’s personal top. Input is the number of interactions between users and items.

Popularity for item \(i\) and user \(u\) is defined as the fraction of actions with item \(i\) among all interactions of user \(u\):

\[Popularity(i_u) = \dfrac{N_iu}{N_u}\]

\(N_iu\) - number of interactions of user \(u\) with item \(i\). \(N_u\) - total number of interactions of user \(u\).

>>> import pandas as pd
>>> data_frame = pd.DataFrame({"user_idx": [1, 1, 3], "item_idx": [1, 2, 3], "relevance": [2, 1, 1]})
>>> data_frame
   user_idx  item_idx  relevance
0         1         1          2
1         1         2          1
2         3         3          1

>>> from replay.utils import convert2spark
>>> data_frame = convert2spark(data_frame)
>>> model = UserPopRec()
>>> res = model.fit_predict(data_frame, 1, filter_seen_items=False)
>>> model.user_item_popularity.count()
3
>>> res.toPandas().sort_values("user_idx", ignore_index=True)
   user_idx  item_idx  relevance
0         1         1   0.666667
1         3         3   1.000000

Wilson Recommender

Confidence interval for binomial distribution can be calculated as:

\[WilsonScore = \frac{\widehat{p}+\frac{z_{ \frac{\alpha}{2}}^{2}}{2n}\pm z_ {\frac{\alpha}{2}}\sqrt{\frac{\widehat{p}(1-\widehat{p})+\frac{z_ {\frac{\alpha}{2}}^{2}}{4n}}{n}} }{1+\frac{z_{ \frac{\alpha}{2}}^{2}}{n}}\]

Where \(\hat{p}\) – is an observed fraction of positive ratings.

\(z_{\alpha}\) 1-alpha quantile of normal distribution.

class replay.models.Wilson(alpha=0.05)

Calculates lower confidence bound for the confidence interval of true fraction of positive ratings.

relevance must be converted to binary 0-1 form.

>>> import pandas as pd
>>> data_frame = pd.DataFrame({"user_idx": [1, 2], "item_idx": [1, 2], "relevance": [1, 1]})
>>> from replay.utils import convert2spark
>>> data_frame = convert2spark(data_frame)
>>> model = Wilson()
>>> model.fit_predict(data_frame,k=1).toPandas()
   user_idx  item_idx  relevance
0         1         2   0.206549
1         2         1   0.206549

Random Recommender

class replay.models.RandomRec(distribution='uniform', alpha=0.0, seed=None, add_cold=True)

Recommend random items, either weighted by item popularity or uniform.

\[P\left(i\right)\propto N_i + \alpha\]

\(N_i\) — number of users who rated item \(i\)

\(\alpha\) — bigger \(\alpha\) values increase amount of rare items in recommendations.: Must be bigger than -1. Default value is \(\alpha = 0\).

>>> from replay.session_handler import get_spark_session, State
>>> spark = get_spark_session(1, 1)
>>> state = State(spark)

>>> import pandas as pd
>>> from replay.utils import convert2spark
>>>
>>> log = convert2spark(pd.DataFrame({
...     "user_idx": [1, 1, 2, 2, 3, 4],
...     "item_idx": [1, 2, 2, 3, 3, 3]
... }))
>>> log.show()
+--------+--------+
|user_idx|item_idx|
+--------+--------+
|       1|       1|
|       1|       2|
|       2|       2|
|       2|       3|
|       3|       3|
|       4|       3|
+--------+--------+

>>> random_pop = RandomRec(distribution="popular_based", alpha=-1)
Traceback (most recent call last):
 ...
ValueError: alpha must be bigger than -1

>>> random_pop = RandomRec(distribution="abracadabra")
Traceback (most recent call last):
 ...
ValueError: distribution can be one of [popular_based, relevance, uniform]

>>> random_pop = RandomRec(distribution="popular_based", alpha=1.0, seed=777)
>>> random_pop.fit(log)
>>> random_pop.item_popularity.show()
+--------+-----------+
|item_idx|probability|
+--------+-----------+
|       1|        2.0|
|       2|        3.0|
|       3|        4.0|
+--------+-----------+

>>> recs = random_pop.predict(log, 2)
>>> recs.show()
+--------+--------+------------------+
|user_idx|item_idx|         relevance|
+--------+--------+------------------+
|       1|       3|0.3333333333333333|
|       2|       1|               0.5|
|       3|       2|               1.0|
|       3|       1|0.3333333333333333|
|       4|       2|               1.0|
|       4|       1|               0.5|
+--------+--------+------------------+

>>> recs = random_pop.predict(log, 2, users=[1], items=[7, 8])
>>> recs.show()
+--------+--------+---------+
|user_idx|item_idx|relevance|
+--------+--------+---------+
|       1|       7|      1.0|
|       1|       8|      0.5|
+--------+--------+---------+

>>> random_pop = RandomRec(seed=555)
>>> random_pop.fit(log)
>>> random_pop.item_popularity.show()
+--------+-----------+
|item_idx|probability|
+--------+-----------+
|       1|        1.0|
|       2|        1.0|
|       3|        1.0|
+--------+-----------+

__init__(distribution='uniform', alpha=0.0, seed=None, add_cold=True)

Parameters

distribution (str) – recommendation strategy: “uniform” - all items are sampled uniformly “popular_based” - recommend popular items more
alpha (float) – bigger values adjust model towards less popular items
seed (Optional[int]) – random seed
add_cold (Optional[bool]) – flag to add cold items with minimal probability

K Nearest Neighbours

class replay.models.KNN(num_neighbours=10, use_relevance=False, shrink=0.0)

Item-based KNN with modified cosine similarity measure.

__init__(num_neighbours=10, use_relevance=False, shrink=0.0)

Parameters

num_neighbours (int) – number of neighbours
use_relevance (bool) – flag to use relevance values as is or to treat them as 1
shrink (float) – term added to the denominator when calculating similarity

Alternating Least Squares

class replay.models.ALSWrap(rank=10, implicit_prefs=True, seed=None)

Wrapper for Spark ALS.

__init__(rank=10, implicit_prefs=True, seed=None)

Parameters

rank (int) – hidden dimension for the approximate matrix
implicit_prefs (bool) – flag to use implicit feedback
seed (Optional[int]) – random seed

SLIM

SLIM Recommender calculates similarity between objects to produce recommendations \(W\).

Loss function is:

\[L = \frac 12||A - A W||^2_F + \frac \beta 2 ||W||_F^2+ \lambda ||W||_1\]

\(W\) – item similarity matrix

\(A\) – interaction matrix

Finding \(W\) can be splitted into solving separate linear regressions with ElasticNet regularization. Thus each row in \(W\) is optimized with

\[l = \frac 12||a_j - A w_j||^2_2 + \frac \beta 2 ||w_j||_2^2+ \lambda ||w_j||_1\]

To remove trivial solution, we add an extra requirements \(w_{jj}=0\), and \(w_{ij}\ge 0\)

class replay.models.SLIM(beta=0.01, lambda_=0.01, seed=None)

SLIM: Sparse Linear Methods for Top-N Recommender Systems

__init__(beta=0.01, lambda_=0.01, seed=None)

Parameters

beta (float) – l2 regularization
lambda – l1 regularization
seed (Optional[int]) – random seed

Word2Vec Recommender

class replay.models.Word2VecRec(rank=100, min_count=5, step_size=0.025, max_iter=1, window_size=1, use_idf=False, seed=None)

Trains word2vec model where items ar treated as words and users as sentences.

__init__(rank=100, min_count=5, step_size=0.025, max_iter=1, window_size=1, use_idf=False, seed=None)

Parameters

rank (int) – embedding size
min_count (int) – the minimum number of times a token must appear to be included in the word2vec model’s vocabulary
step_size (int) – step size to be used for each iteration of optimization
max_iter (int) – max number of iterations
window_size (int) – window size
use_idf (bool) – flag to use inverse document frequency
seed (Optional[int]) – random seed

Association Rules Item-to-Item Recommender

class replay.models.AssociationRulesItemRec(session_col=None, min_item_count=5, min_pair_count=5, num_neighbours=1000, use_relevance=False)

Item-to-item recommender based on association rules. Calculate pairs confidence, lift and confidence_gain defined as confidence(a, b)/confidence(!a, b) to get top-k associated items.

Classical model uses items co-occurrence in sessions for confidence, lift and confidence_gain calculation but relevance could also be passed to the model, e.g. if you want to apply time smoothing and treat old sessions as less important. In this case all items in sessions should have the same relevance.

__init__(session_col=None, min_item_count=5, min_pair_count=5, num_neighbours=1000, use_relevance=False)

Parameters

session_col (Optional[str]) – name of column to group sessions. Items are combined by the user_id column if session_col is not defined.
min_item_count (int) – items with fewer sessions will be filtered out
min_pair_count (int) – pairs with fewer sessions will be filtered out
num_neighbours (Optional[int]) – maximal number of neighbours to save for each item
use_relevance (bool) – flag to use relevance values instead of co-occurrence count If true, pair relevance in session is minimal relevance of item in pair. Item relevance is sum of relevance in all sessions.

get_nearest_items(items, k, metric='lift', candidates=None)

Get k most similar items be the metric for each of the items.

Parameters

items (Union[DataFrame, Iterable]) – spark dataframe or list of item ids to find neighbors
k (int) – number of neighbors
metric (Optional[str]) – lift of ‘confidence_gain’
candidates (Union[DataFrame, Iterable, None]) – spark dataframe or list of items to consider as similar, e.g. popular/new items. If None, all items presented during model training are used.

Return type

DataFrame

Returns

dataframe with the most similar items an distance, where bigger value means greater similarity. spark-dataframe with columns [item_id, neighbour_item_id, similarity]

Cluster Recommender

class replay.models.ClusterRec(num_clusters=10)

Generate recommendations for cold users using k-means clusters

__init__(num_clusters=10)

Parameters: num_clusters (int) – number of clusters

Neural models with distributed inference

Models implemented in pytorch with distributed inference in pyspark.

Neural Matrix Factorization

class replay.models.NeuroMF(learning_rate=0.05, epochs=20, embedding_gmf_dim=None, embedding_mlp_dim=None, hidden_mlp_dims=None, l2_reg=0, gamma=0.99, count_negative_sample=1)

Neural Matrix Factorization model (NeuMF, NCF).

In this implementation MLP and GMF modules are optional.

__init__(learning_rate=0.05, epochs=20, embedding_gmf_dim=None, embedding_mlp_dim=None, hidden_mlp_dims=None, l2_reg=0, gamma=0.99, count_negative_sample=1)

MLP or GMF model can be ignored if its embedding size (embedding_mlp_dim or embedding_gmf_dim) is set to None. Default variant is MLP + GMF with embedding size 128.

Parameters

learning_rate (float) – learning rate
epochs (int) – number of epochs to train model
embedding_gmf_dim (Optional[int]) – embedding size for gmf
embedding_mlp_dim (Optional[int]) – embedding size for mlp
hidden_mlp_dims (Optional[List[int]]) – list of hidden dimension sized for mlp
l2_reg (float) – l2 regularization term
gamma (float) – decrease learning rate by this coefficient per epoch
count_negative_sample (int) – number of negative samples to use

Mult-VAE

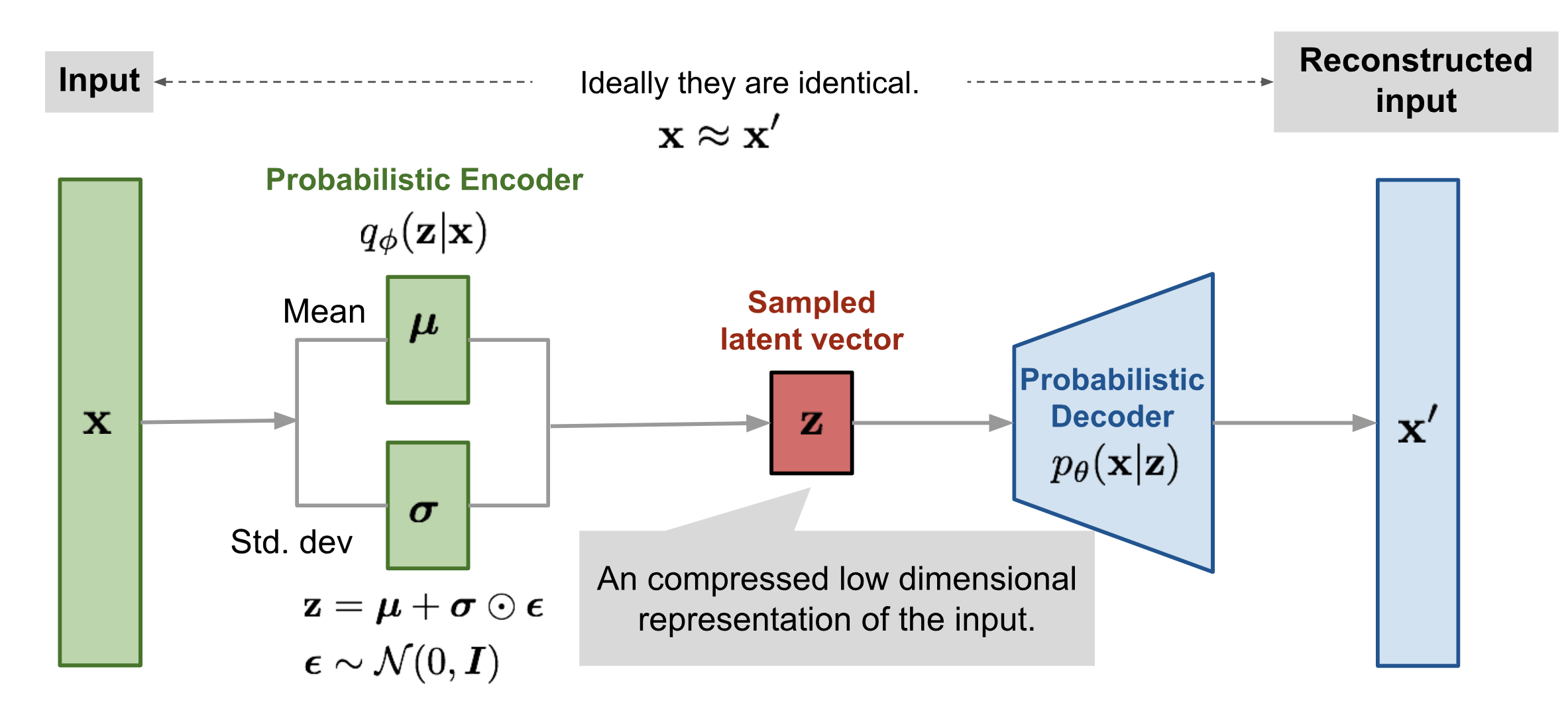
Variation AutoEncoder

Problem formulation

We have a sample of independent equally distributed random values from true distribution \(x_i \sim p_d(x)\), \(i = 1, \dots, N\).

Build a probability model \(p_\theta(x)\) for true distribution \(p_d(x)\).

Distribution \(p_\theta(x)\) allows both to estimate probability density for a given item \(x\), and to sample \(x \sim p_\theta(x)\).

Probability model

\(z \in \mathbb{R}^d\) - is a local latent variable, one for each item \(x\).

Generative process for variational autoencoder:

Sample \(z \sim p(z)\).
Sample \(x \sim p_\theta(x | z)\).

Distribution parameters \(p_\theta(x | z)\) are defined with neural net weights \(\theta\), with input \(z\).

Item probability density \(x\):

\[p_\theta(x) = \mathbb{E}_{z \sim p(z)} p_\theta(x | z)\]

Use lower estimate bound for the log likelihood.

\[\begin{split}\log p_\theta(x) = \mathbb{E}_{z \sim q_\phi(z | x)} \log p_\theta( x) = \mathbb{E}_{z \sim q_\phi(z | x)} \log \frac{p_\theta(x, z) q_\phi(z | x)} {q_\phi(z | x) p_\theta(z | x)} = \\ = \mathbb{E}_{z \sim q_\phi(z | x)} \log \frac{p_\theta(x, z)}{q_\phi(z | x)} + KL( q_\phi(z | x) || p_\theta(z | x))\end{split}\]

\[\begin{split}\log p_\theta(x) \geqslant \mathbb{E}_{z \sim q_\phi(z | x)} \log \frac{p_\theta(x | z)p(z)}{q_\phi(z | x)} = \mathbb{E}_{z \sim q_\phi(z | x)} \log p_\theta(x | z) - KL(q_\phi(z | x) || p(z)) = \\ = L(x; \phi, \theta) \to \max\limits_{\phi, \theta}\end{split}\]

\(q_\phi(z | x)\) is a proposal or a recognition distribution. It is a gaussian with weights \(\phi\): \(q_\phi(z | x) = \mathcal{N}(z | \mu_\phi(x), \sigma^2_\phi(x)I)\).

Difference between lower estimate bound \(L(x; \phi, \theta)\) and log likelihood \(\log p_\theta(x)\) - is a KL-divergence between a proposal and aposteriory distribution on \(z\): \(KL(q_\phi(z | x) || p_\theta(z | x))\). Maximum value \(L(x; \phi, \theta)\) for fixed model parameters \(\theta\) is reached with \(q_\phi(z | x) = p_\theta(z | x)\), but explicit calculation of \(p_\theta(z | x)\) is not efficient to calculate, so it is also optimized by \(\phi\). The closer \(q_\phi(z | x)\) to \(p_\theta(z | x)\), the better the estimate.

We usually take normal distribution for \(p(z)\):

\[\varepsilon \sim \mathcal{N}(\varepsilon | 0, I)\]

\[z = \mu + \sigma \varepsilon \Rightarrow z \sim \mathcal{N}(z | \mu, \sigma^2I)\]

\[\frac{\partial}{\partial \phi} L(x; \phi, \theta) = \mathbb{E}_{ \varepsilon \sim \mathcal{N}(\varepsilon | 0, I)} \frac{\partial} {\partial \phi} \log p_\theta(x | \mu_\phi(x) + \sigma_\phi(x) \varepsilon) - \frac{\partial}{\partial \phi} KL(q_\phi(z | x) || p(z))\]

\[\frac{\partial}{\partial \theta} L(x; \phi, \theta) = \mathbb{E}_{z \sim q_\phi(z | x)} \frac{\partial}{\partial \theta} \log p_\theta(x | z)\]

In this case

\[KL(q_\phi(z | x) || p(z)) = -\frac{1}{2}\sum_{i=1}^{dimZ}(1+ log(\sigma_i^2) - \mu_i^2-\sigma_i^2)\]

KL-divergence coefficient can also not be equal to one, in this case:

\[L(x; \phi, \theta) = \mathbb{E}_{z \sim q_\phi(z | x)} \log p_\theta(x | z) - \beta \cdot KL(q_\phi(z | x) || p(z)) \to \max\limits_{\phi, \theta}\]

With \(\beta = 0\) VAE is the same as the Denoising AutoEncoder.

class replay.models.MultVAE(learning_rate=0.01, epochs=100, latent_dim=200, hidden_dim=600, dropout=0.3, anneal=0.1, l2_reg=0, gamma=0.99)

Variational Autoencoders for Collaborative Filtering

__init__(learning_rate=0.01, epochs=100, latent_dim=200, hidden_dim=600, dropout=0.3, anneal=0.1, l2_reg=0, gamma=0.99)

Parameters

learning_rate (float) – learning rate
epochs (int) – number of epochs to train model
latent_dim (int) – latent dimension size for user vectors
hidden_dim (int) – hidden dimension size for encoder and decoder
dropout (float) – dropout coefficient
anneal (float) – anneal coefficient [0,1]
l2_reg (float) – l2 regularization term
gamma (float) – reduce learning rate by this coefficient per epoch

Wrappers and other models with distributed inference

Wrappers for popular recommendation libraries and algorithms implemented in python with distributed inference in pyspark.

ADMM SLIM

class replay.models.ADMMSLIM(lambda_1=5, lambda_2=5000, seed=None)

ADMM SLIM: Sparse Recommendations for Many Users

This is a modification for the basic SLIM model. Recommendations are improved with Alternating Direction Method of Multipliers.

__init__(lambda_1=5, lambda_2=5000, seed=None)

Parameters

lambda_1 (float) – l1 regularization term
lambda_2 (float) – l2 regularization term
seed (Optional[int]) – random seed

LightFM

class replay.models.LightFMWrap(no_components=128, loss='warp', random_state=None)

Wrapper for LightFM.

__init__(no_components=128, loss='warp', random_state=None)

implicit

class replay.models.ImplicitWrap(model)

Wrapper for implicit

Example:

>>> import implicit
>>> model = implicit.als.AlternatingLeastSquares(factors=5)
>>> als = ImplicitWrap(model)

This way you can use implicit models as any other in replay with conversions made under the hood.

>>> import pandas as pd
>>> from replay.utils import convert2spark
>>> df = pd.DataFrame({"user_idx": [1, 1, 2, 2], "item_idx": [1, 2, 2, 3], "relevance": [1, 1, 1, 1]})
>>> df = convert2spark(df)
>>> als.fit_predict(df, 1, users=[1])[["user_idx", "item_idx"]].toPandas()
   user_idx  item_idx
0         1         3

__init__(model): Provide initialized implicit model.